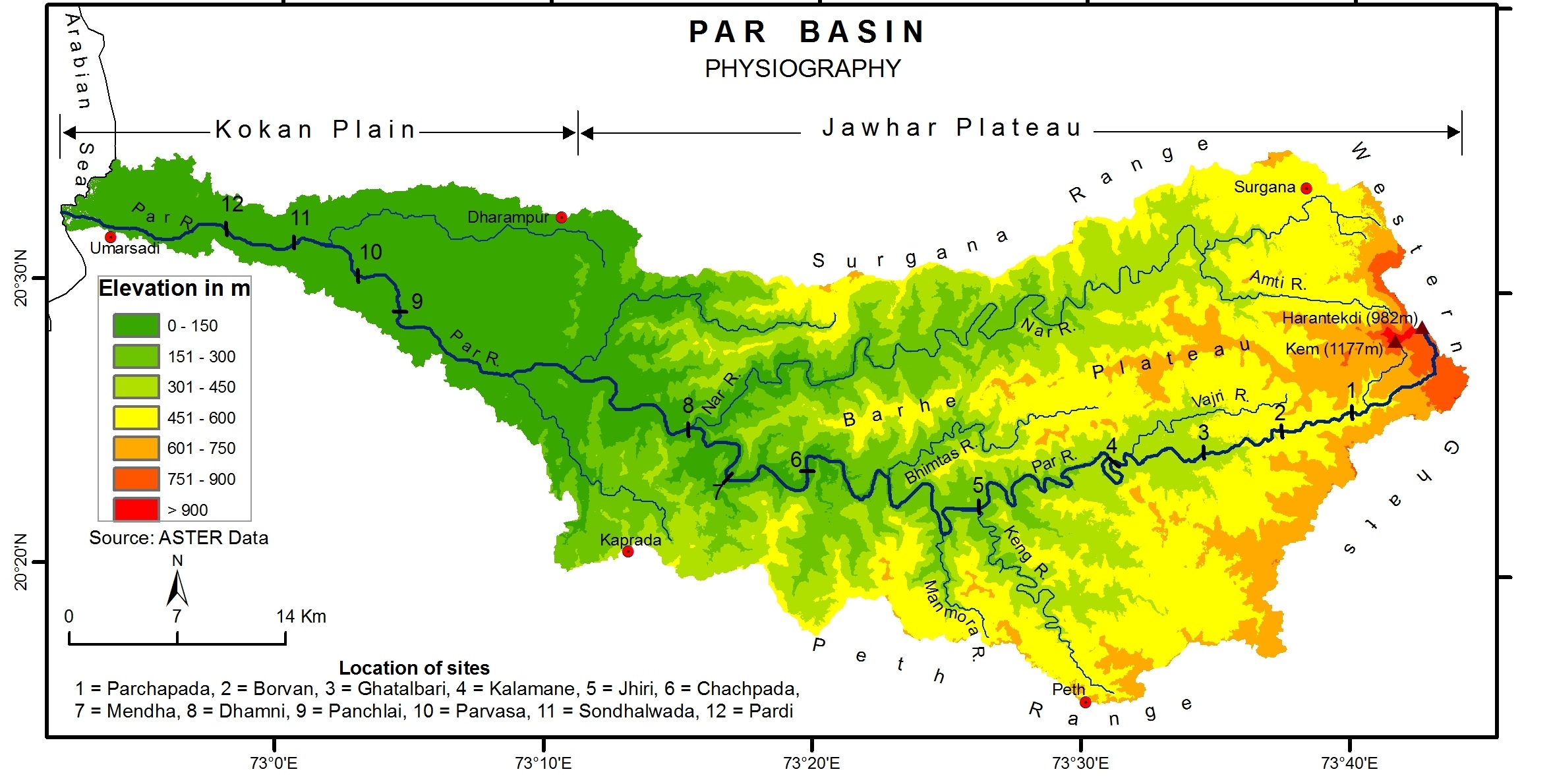
Hydrologic and Geomorphic Aspects of High-magnitude Floods on the Par River in Western India

 ,
Priyanka Hire 2
,
Priyanka Hire 2
 ,
Pramodkumar Hire 3
,
Pramodkumar Hire 3


1.RNC Arts, JDB Commerce and NSC Science College, Nashik Road, India
2.Department of Geography, HPT Arts and RYK Science College, Nashik, India
3.Department of Geography, HPT Arts and RYK Science College, Nashik - 422 005 (Maharashtra), India.


*.Department of Geography, HPT Arts and RYK Science College, Nashik - 422 005.


1.Department of Geography, HPT Arts and RYK Science College, Nashik - 422 005.