Keywords

Stable land objects , Forest change detection , Tasseled Cap Coefficient , LST , NDVI , Landsat-7 ETM+ , Landsat-5 TM

1 . INTRODUCTION

A forest is a community of living organisms which interact mutually with the physical environment. Forest covers approximately 30% (Carlowicz, 2012) to 31% (FAO, 2015) of the earth surface with complexities and self-regenerating capacities (Bauer et al., 1994; Virk and King, 2006; Healey et al., 2008). It is a source of organic carbon, which helps to maintain planetary climate, freshwater, biodiversity and useful to manage hazards like soil erosion, landslides, floods, etc. They are habitat of wildlife and regulate different cycles including hydrological, nutrient, atmospheric, etc. and conserve soils, water, etc. (Southworth, 2004).

Land under natural forest is estimated about 33.36 million km² (World Resources Institute [WRI]) to 39.88 million km² (World Conservation Monitoring Centre [WCMC]) excluding marine forests (Mishra et al., 2003; Kumsap et al., 2005; Fettig et al., 2007; Forkuo and Frimpong, 2012). However, from last some decades forest destruction and land appropriation increase, globally (Turker and Derenyi, 2000). Land under forest in India declined to 21.31% of Total Geographical Area (TGA) (ISFR, 2009 and FSI 2015) due to imbalance climatic conditions, soil degradation, deforestation, desertification and water stresses in drought conditions. India endowed with an immense variety of forest resources (Southworth, 2004). However, adverse changes in ecosystem are taking place with continuous pressures of an exploding population and the subsequent domestic needs including food, fuel, fodder, timber as well as industrial demands (Keenan et al., 1999). There are significant losses of forests at an alarming rate (Pant et al., 2000; Hayes and Sader, 2001). The ‘hotspots’ are identified and declared for tropical biodiversity in Western Ghats. These regions are house of rich biodiversity and globally endemic species (Fang and Xu, 2000). However, it is widely believed that the natural vegetation in this tropical region is losing the biodiversity at unprecedented rates (Panigrahy et al., 2010). Around, 275 million rural people (27%) in India are depends on forests for their subsistence and livelihoods (Kim et al., 2011), earning from trade of fuel wood, fodder, bamboo and minor forest products. It is notable that 17% of rural population in India depends on forests to meet their domestic energy (Drescher and Perera, 2010).

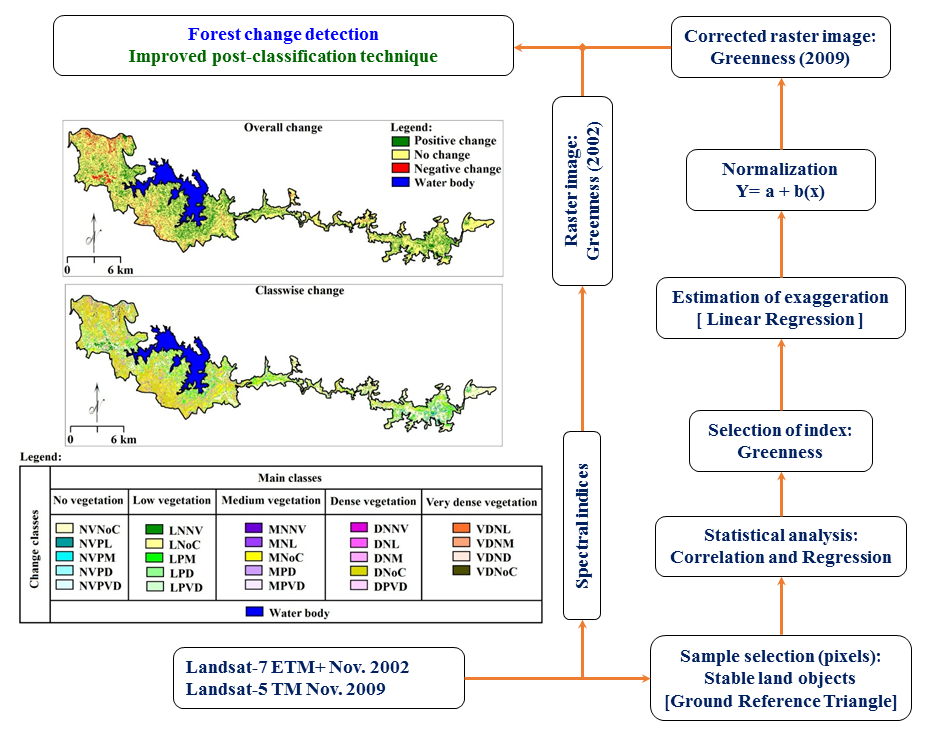
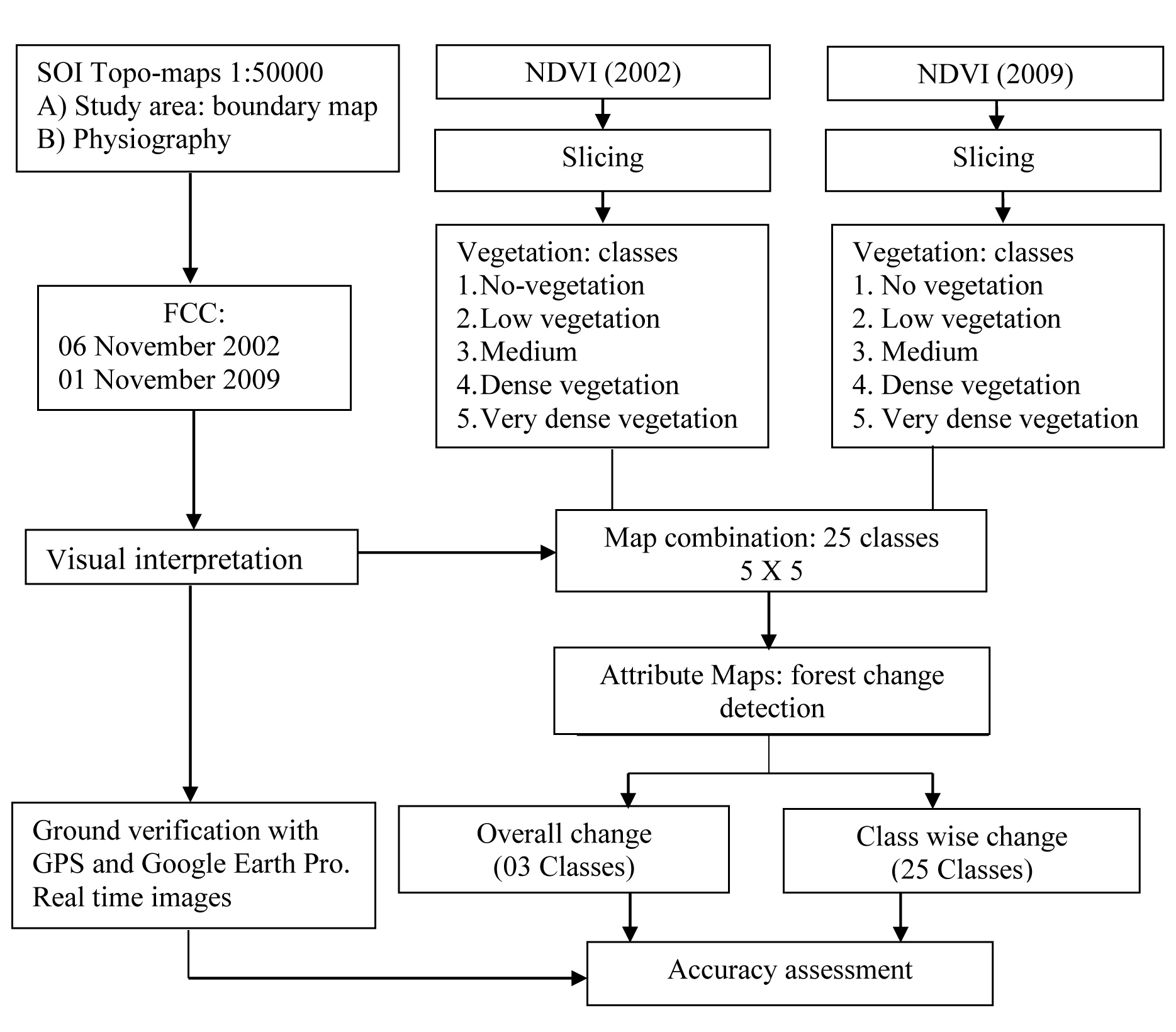
Governmental and non-governmental agencies are involved in conservation of forests from last some decades (Cohen et al., 1998). Planning and management for conservation of forest demands reliable information, investigation and analyses (Cohen et al., 1998; Hansen et al., 2000, Hayes and Sader, 2001; Bhagat, 2009). Many analysts have reported sophisticated techniques like remote sensing (Kennedy et al., 2009), geographic information system (Healey et al., 2008), global positioning system along with mathematical and statistical methods (Fettig et al., 2007) for change detection. Estimations of forests cover using satellite data can give satisfactorily results (Cano et al., 2006). Furthermore, change detection analysis can provide analytical data about forest degradation and conservation (Pouliot et al., 2002). However, reliable change detection techniques for forests using remote sensing data remains a challenging task (Coppin et al., 2004; Im et al.,2008;  Schwilch et al., 2011; Sommer et al., 2011; Bhagat, 2012). The results are susceptible to data quality, technical efficiency and suitability of selected techniques (Bhagat, 2012). Therefore, modified change detection technique designed for this study based on field checks and statistical analyses to get more precise analysis about forest changes (Southworth, 2004). The Landsat-5 TM and Landsat-7 ETM+ datasets have been used for detection of changes in forest cover in the study area. Two approaches have been adopted for this analysis: Approach I) post-classification technique and Approach II) improved post-classification technique (Chandio and Matori, 2011). Changes in forest were detected using post-classification techniques using NDVI (Fettig et al., 2007) calculated for Landsat-5 TM and Landsat-7 ETM+ datasets, whereas normalized indices and coefficients were used for improved approach of change detection.

Change detection analysis provides a thematic views to understand the natural and artificial behaviour of changes in land (Sommer et al., 2011) including 1) increase and decrease in area, 2) seasonal changes in forests, snow cover, coastline, ocean water, 3) mapping of floods, landslides, volcanic eruptions, corral rifts, wild animals, birds, 4) changes in near surface atmospheric conditions like temperature, snowfall, rainfall, clouds, fog, storms, and 5) human activities like military actions, observation, planning and management for war areas, coal mining, etc. (Lunetta et al., 2006). Scientists have used different methods of Digital Change Detection (DCD) including classification of multiband satellite data based on image ratio, tasseled cap coefficient, spectral vegetation indices, principal component analysis, change vector methods, threshold based classification, post-classification comparison, univariate image differencing, simultaneous analysis of multi temporal data, fusion approach, spectral classification, algebraic methods, regressions, etc. (Petit and Lambin, 2001; Bhagat, 2012). However, all methods are not ideally suitable, reliable and applicable to all surface change conditions (Du et al., 2002; Bhagat, 2012). Therefore, corrective measure has been suggested to achieve more precise results of forest change detection in this study. Correlation techniques have been used to find the suitable parameter for corrections from different multiband ratios (Coppin and Bauer, 1996) and spectral indices (Huete et al., 2002). Here, correlation and regression (Mountrakis et al., 2010) techniques have been used to determine variables for detection, estimations of exaggerations and corrections using information collected for stable land surface (water bodies, rocky lands, deep forest, etc.). The suggested technique for forest change detection can be useful for land management and especially forests.

2 . STUDY AREA

The study area (13859 ha) is a mountainous range between Pravara and Mula river basin from Western (Ghatghar) to Eastern borders (Washere) of Akole tahsil in Ahmednagar District (India) (Figure 1). The altitude varies from 560 to 1646 m Mean Sea Level (MSL). Geologically, this area is formed by basaltic rock (Gareeau et al., 2009) which prevents water to percolate. The depth and water-holding capacity of soils in the region (Zolekar and Bhagat, 2015) varies according to variations in slopes. The soils are very shallow at hilltop and depth increasing to foothill zones (Kumsap et al., 2005). Very shallow loamy, shallow clayey soils are found on the moderate (1°- 3°) and stiff (3°- 6°) slopes. Soil moisture impacts on the distribution of vegetation cover (Mishra et al., 2003). The forest cover varies with height, slopes, soil qualities, rainfall, etc. Foothill zones in Western parts show dense forest than hilltops with thin soils. Annual rainfall varies from 4937 mm at West and 1904 mm at East (Zolekar and Bhagat, 2015). The mean annual maximum and minimum temperatures are 39.80°C and 8.70°C, respectively. Indigenous people are engaged in agricultural activities (Theiler and Perkins, 2011) on land reclaimed from forests and dependent on forests for domestic needs. 

Figure 1. Study area: location map

3 . DATASET AND SOFTWARE

4 . METHODOLOGY AND APPROACHES

4.2.1 Spectral Indices

In present study, Difference Vegetation Index (DVI), Ratio Vegetation Index (RVI), NDVI, Soil Adjusted Vegetation Index (SAVI), Leaf Area Index (LAI), Ratio Difference Vegetation Index (RDVI), Modified SAVI (MSAVI), Infrared Percentage Vegetation Index (IPVI) and Modified Simple Ratio (MSR) (Mróz and Sobieraj, 2004) have been used for change detection analysis. However, NDVI has been widely used for detection of changes in forest cover (Bhagat, 2012). Therefore, NDVI (equation 1) has been calculated using Near Infrared (Band 4) and Red (Band 3) bands of Landsat-7 ETM+ and Landsat-5 TM sensors (Bhagat and Sonawane, 2010).

  \(NDVI = {NIR-RED \over NIR+RED}\)                   (1)

Calculated NDVI values vary between -1 to +1 depending on relative Digital Number (DN) of Near Infrared and Red bands. Maximum NDVI (Figure 2) indicates dense vegetation and minimum values represent less or absence of vegetation. 

Figure 2. Normalized Difference Vegetation Index (NDVI)

Leaf Area Index (LAI) [m²/m²] represents the amount of leaf material in an ecosystem and is geometrically defined as the total one-sided area of photosynthetic tissue per unit ground surface area (Breda, 2003; Jonckheere et al., 2004; Morisette et al., 2006). It appears as a key variable in many models describing vegetation-atmosphere interactions, particularly with respect to the carbon and water cycles (GCOS, 2010). LAI was calculated using following equation after Jensen (2002) (equation 2):

\(LAI = -2.42 +12.18 *(NDVI)\)        (2)

Where, -2.42 and 12.18 are the constants (Jensen, 2002). LAI is widely used to identify and delineate light interception, gross productivity, soil moisture and transpiration from vegetation (Chen et al., 2012). Therefore, LAI were calculated for statistical analysis to test applicability for Forest Change Detection (FCD) in second approach. Furthermore, many scholars have been used Land Surface Temperature Index (LSTI) for vegetation analysis (Yuan and Bauer, 2007). LSTI is measurements of earth surface temperature including  canopy, soils, barren lands, rocks, water bodies, snow, ice, roof of a building using satellite data. The DN recorded for satellite images (Julien et al., 2011) were converted (equation 3) using space reaching radiance i.e. Top of Atmosphere (ToA) Radiance (equation 4) (Chander and Markham, 2003).

\(LST(T) = {{K_2} \over in({k_1\over L_\lambda}+1)}\)                           (3)

Here, \(T\)  is an effective at-satellite temperature in k (kelvin), \(L_\lambda\) is a spectral radiance in W/(m² in µm), \(K_1\) and \(K_2\) are pre-launch calibration constants for ETM+ and TM sansors.

   \(L_\lambda = ({{L_{max}-L_{min}} \over QCAL_{max}-QCAL_{min}})(DN-QCAL_{min})+L_{min}\)       (4)

Where, \(L_{max}\)  is a maximum spectral radiance (W/m² in µm) at QCAL equal 0 DN, \(L_{mim}\) is a minimum spectral radiance (W/m² in µm) at QCAL equal 255 DN and QCAL are the quantized calibrated pixel values in DN.

4.2.2 Tasseled Cap Coefficient Transformations (TCCTs)

TCCTs have potentials to derive forest attributes for different regional applications where, atmospheric noise correction not possible (Silleos et al., 2006; Ghosh et al., 2010). These transformations simply reduce the number of radiance noise density and provide high association in single response. Therefore, brightness, greenness, wetness, fourth, fifth and sixth indices were calculated using coefficients estimated by Crist et al., (1986) for Landsat-5 TM (Table 1) and Huang et al., (2002) (Table 2) for Landsat-7 ETM+. 

4.3   Approaches of Forest Change Detection

4.3.1 Approach I: Post-classification technique

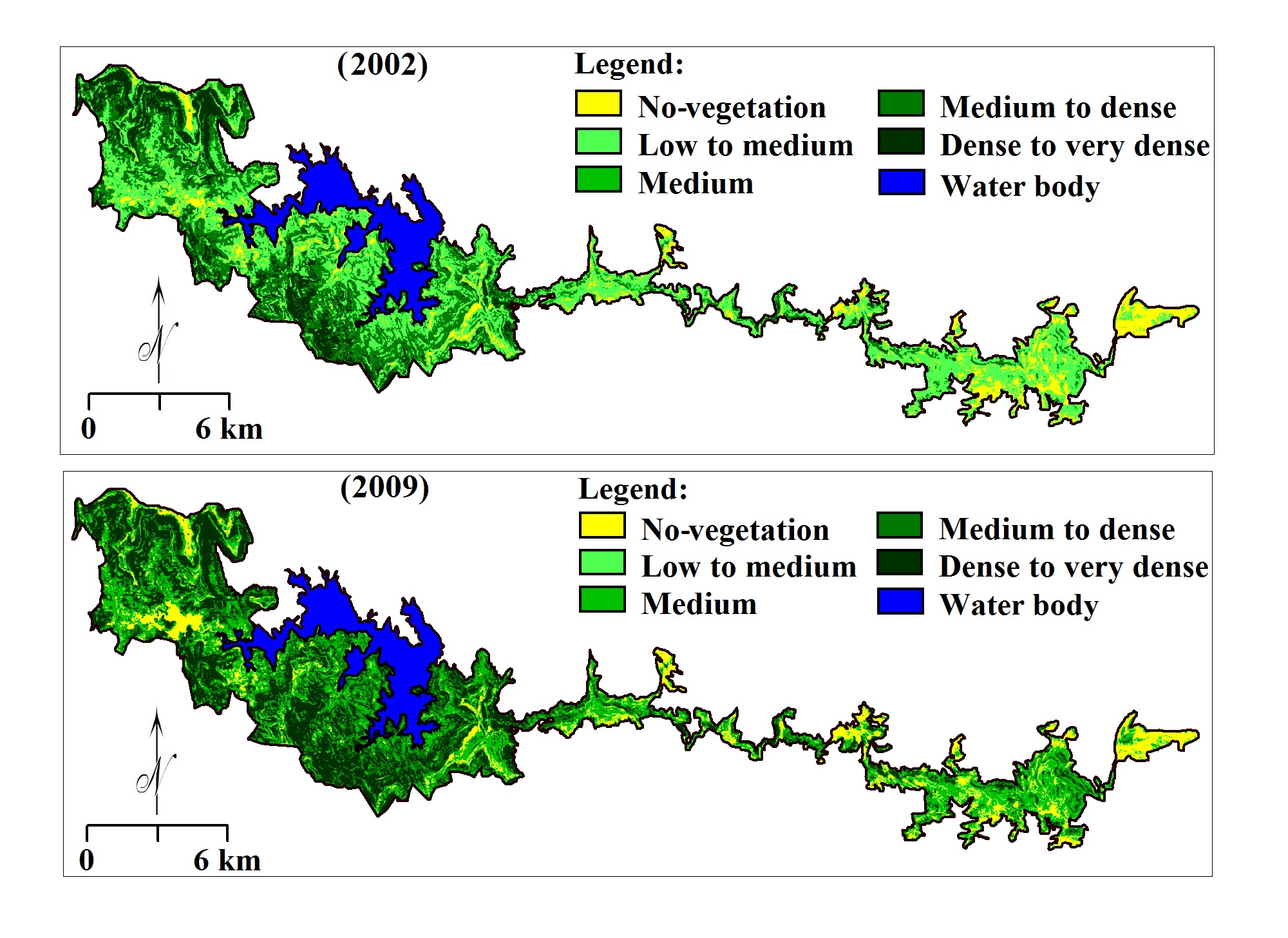
Satellite images selected for present study was processed for co-registration, enhancements, classification and finally, classified images were compared for Change Detection (CD) in forest cover. Calculated pixel values of NDVI have been broadly grouped into five classes (Table 3) i.e. no-vegetation, low to medium, medium, medium to dense and dense to very dense, using threshold observed in NDVI (2002) and NDVI (2009) images using ‘slicing’ operation in Ilwis.

The maximum value (0.41) in reference image (t₁) (NDVI 2002) was observed for dense vegetation (Table 3) whereas minimum (-0.48) for barren land including water body, rocky and barren land with 0.05 mean and 0.16 standard deviation. Targeted image (t₂) (NDVI 2009) shows the maximum value (0.71) for dense vegetation and minimum (-0.33) for no-vegetation with 0.31 mean and 0.16 standard deviation. Adegoke and Carleton (2002) have been used innovative hybrid image classification technique for change detection analysis of forest. Therefore, limit values of NDVI classes are different for images acquired for 2002 and 2009 (Table 3) and was decided based on repetitive field checks using GPS, comparison with high-resolution images of Google Earth Pro and FCC (Figure 4). Class ‘no-vegetation’ includes rocky and barren lands distributed at higher levels (> 1100 m) of mountain and water bodies at bottom (Figure 3). 

Figure 3. Distribution of forest depicted based on NDVI

Figure 4. False Color Composite (FCC) images

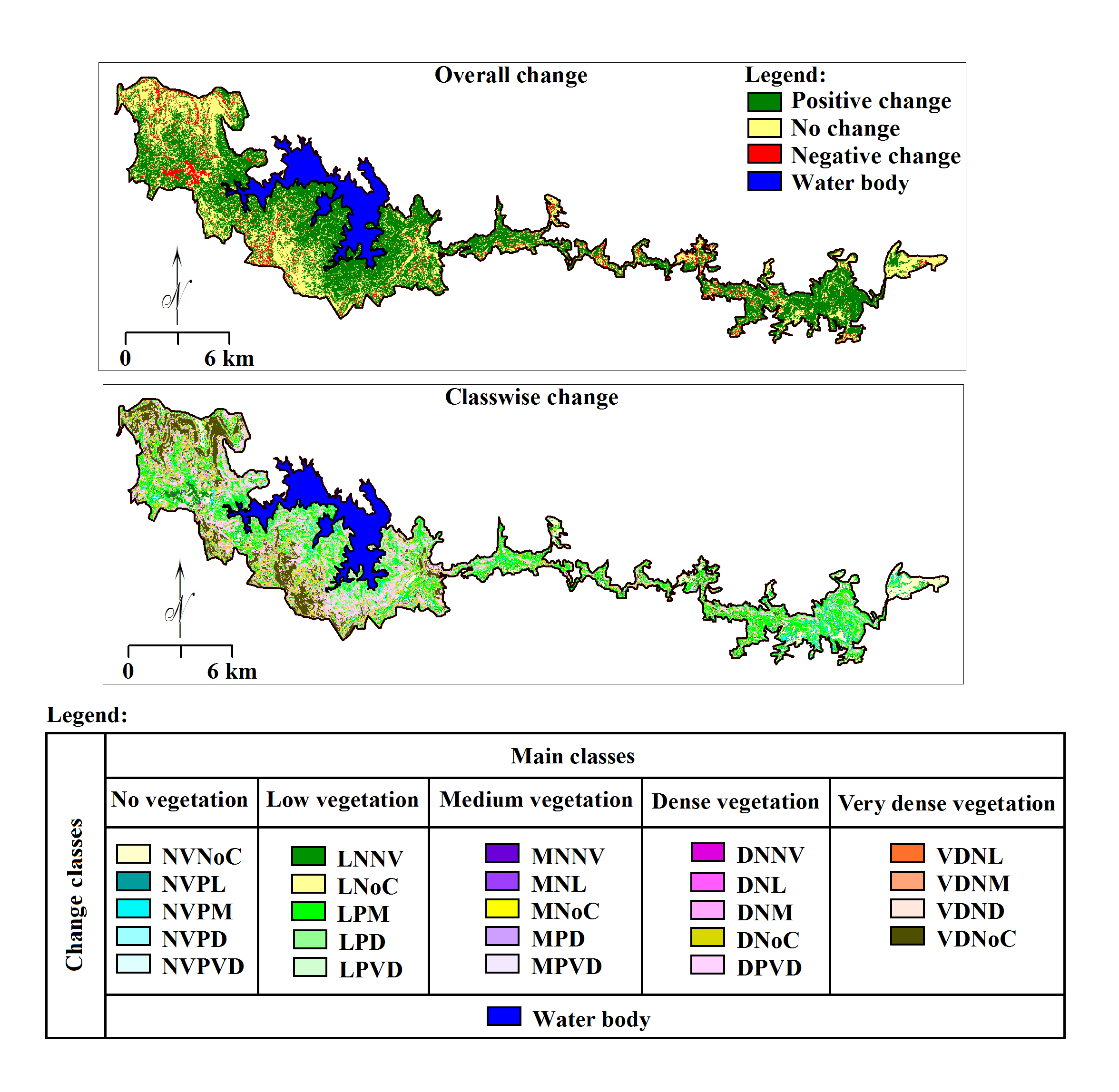
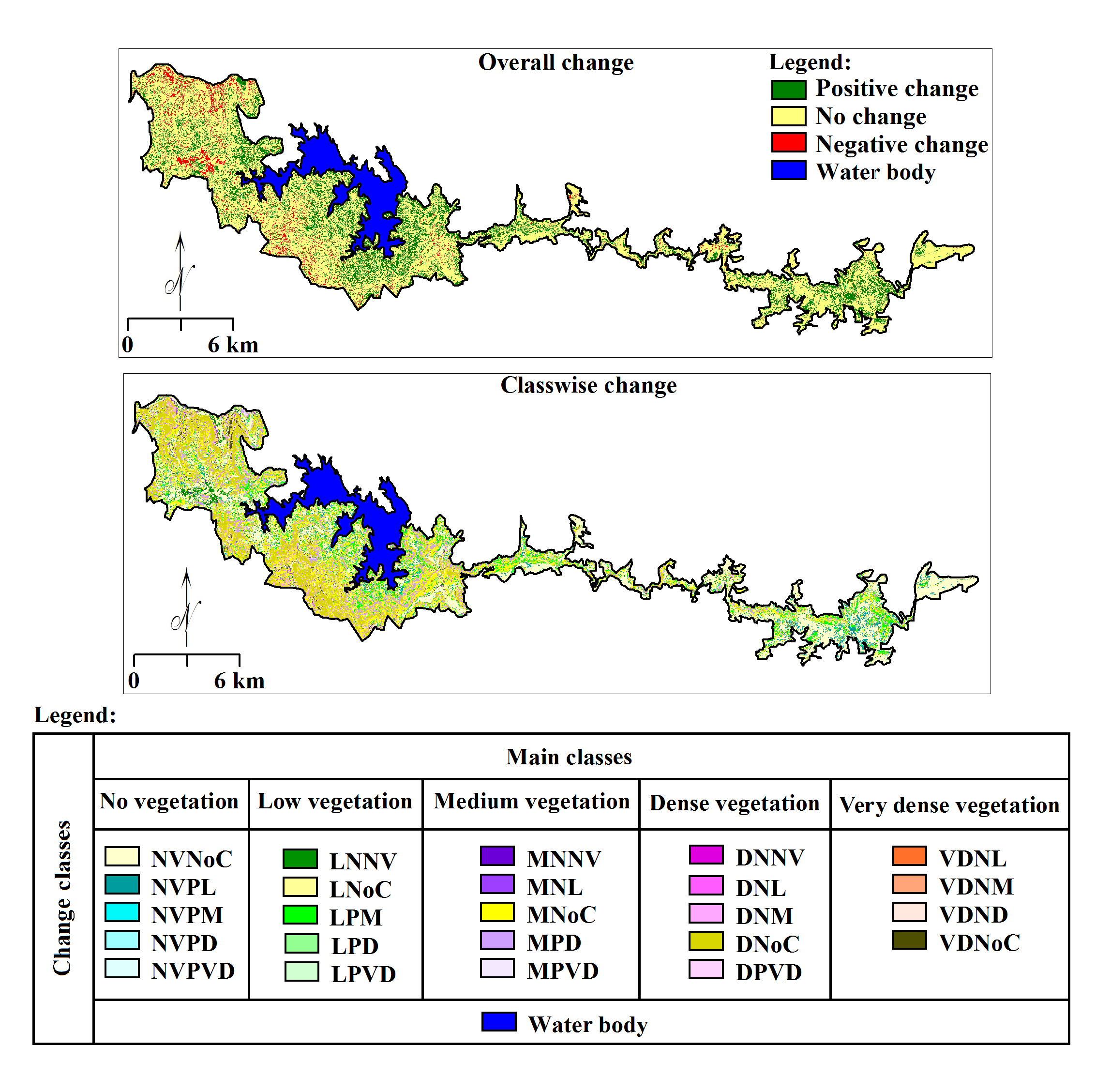
Measurements of differences between detected land classes in base image (t₁) and target image (t₂) based on radiance difference called change detection (Weng et al., 2009), for instance forest. The radiance difference mainly occurred due to real change in surface features, deviation in atmospheric conditions, deviation in sensor calibration, minimum to maximum error in Route Mean Square (RMS) at the time of georeferencing, deviation in illumination and difference in soil moisture conditions, etc. Here, classified images t₁ and t₂ combined using ‘cross’ operator (Figure 5) in Ilwis which produce 25 classes (5 classes t₁ X 5 classes t₂). Similar classes have been merged into three classes viz. no-change, positive change and negative change in forest cover (Table 4) using tool ‘merging the classes’ in Ilwis. Further, class wise changes (Table 11) in forest cover also detected successfully (Figure 14) using same technique (Table 4). However, overall accuracy of the classes detected to show changes in forest cover was estimated about 78%. Users’ accuracy for class ‘positive change’ was about 58% and producer’s accuracy 70%. Rozenstein and Karnieli (2011) have insisted vigorous and creative efforts to establish new algorithms for change detection. Therefore, statistical methods and corrective measures were adopted to achieve improvements in post-classification technique for CD in forest cover. 

Figure 5. Approach-I: schematic preparation

4.3.2  Approach II: Improved post-classification technique

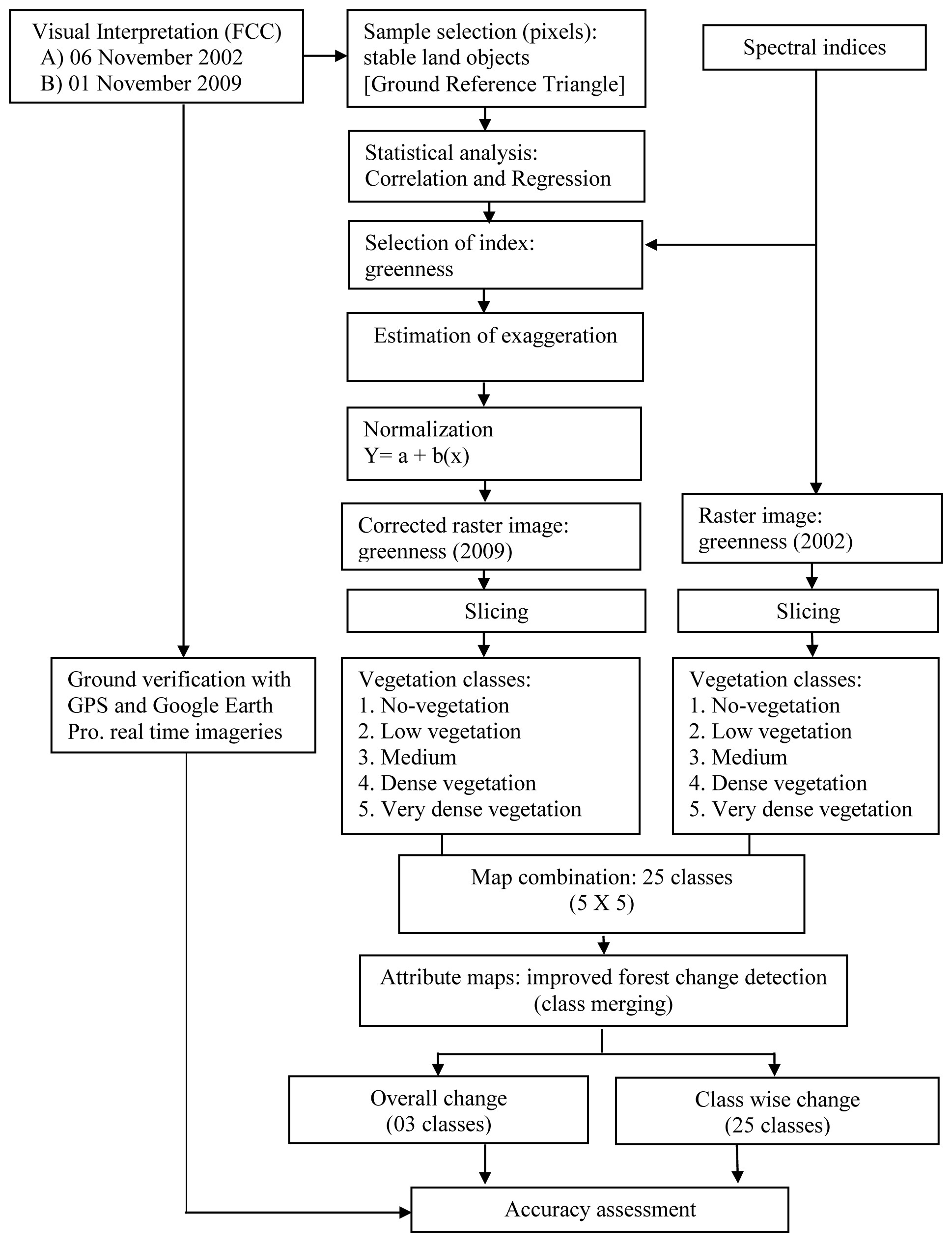
Many scholars have been successfully used combinations of different approaches for CD of land objects (Cano et al., 2006; Pu et al., 2008; Weng et al., 2009). The algorithm of FCD has been modified to improve (Figure 6) the results and processed through five steps: 1) sampling (Chapelle et al., 2002; Lu et al., 2011), 2) statistical analysis (Singh, 1989; Dhakal et al., 2002), 3) normalization of indices, 4) change detection and 5) accuracy assessment. Statistical analysis and information about stable land surface including deep forests, rocky lands, barren lands and water bodies have used for normalization of indices calculated for target image (t₂) (Felkar et al., 1981; Singh, 1996; Turker and Derenyi, 2000). 

Figure 6. Approach-II: schematic preparation

a. Sampling

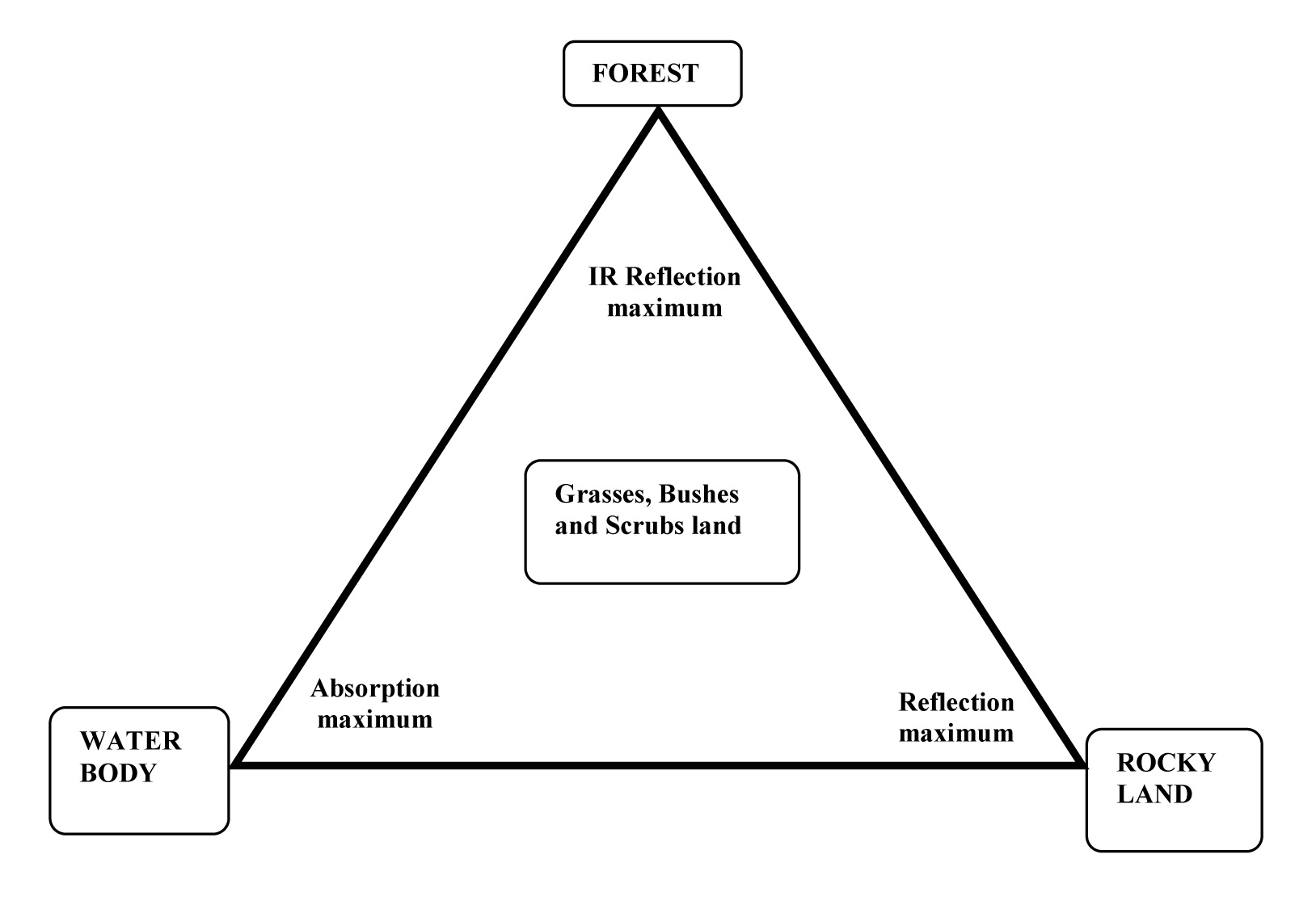
Many researchers have been successfully used single band, ratio indices and coefficients for detection and delineation (Chen et al., 2012) of objects like forests, water bodies, barren lands, rocky lands, snow covers, marsh lands, desert lands, etc. The variations in land phenomenon regulate surface radiance according to their reflectivity (Carlson et al., 1990; Chen et al., 2012). Surface reflectance values are sensitive to variations in vegetation cover, soil, background temperature, thermal inertia, and topography (Bhagat 2012). Goetz (1997) has used inverse relationship between SVI and Ts based on inversion soil-vegetation-atmosphere-transfer (SVAT) model for estimating soil surface moisture using NDVI-Ts triangle space. This approach is defined as the ‘Triangle Method’ includes vegetation indices, soil moisture indices and thermal indices (Weng et al., 2009; Lu et al., 2011). Objects detected using this approach are stood more precise than single bands. Surface temperature can be estimated using thermal band and vegetation can be detected with the help of near infrared band (Nemani and Running, 1989; Carlosan et al., 1990; Nemani et al., 1993; Tanriverdi, 2010). Thus, all surface elements have equal importance in estimations of objects (Owen et al., 1998).

Water body absorbs maximum amount of radiation and emits very little energy (Nemani et al., 1993). Forest cover reflects maximum amount of Green and Near Infrared (NIR) bands and a good absorber of Blue and Red band. Chemical component existing in tree leaves known as ‘chlorophyll’ effectively absorbs radiation from the Blue and Red band (Jiany et al., 2008). The inner structure of these leaves response as good emission of NIR wavelength (Roberts et al., 2011). On the other hand, visible and NIR radiation absorb more in the form of longer wavelength from water body and less from shorter wavelength (Lu et al., 2011). Thus, water appears blue-green or blue due to maximum reflectance of shorter wavelength and viewed dark because reflectance of red and near infrared depending on the suspended sediments amount in water (Fletcher and Everitt, 2007). Rocky lands are purely dry and rarely covered by thin grass and algae in wet seasons. However, rocky lands absorb very low amount of visible as well as NIR waves and reflect maximum as compare to other classes (Majed et al., 2011). Water bodies, deep forests and rocky lands are stable objects and have extreme reflectance (minimum and maximum) in the region.

The variations in reflectance recorded is satellite image have influence on accuracy of forest CD using post-classification (Pu et al., 2008). Therefore, corrective approach was adopted for detection of FCD (discussed in next section). Ground truth information (170 samples) was collected for these stable land objects which were appeared and identified on satellite images e.g. Landsat-7 ETM+ (2002) and Landsat-5 TM (2009). DN values of these land objects were used further statistical analysis and normalisation of indices calculated using satellite data (t₂) (Bhagat, 2012). About 31.18% samples were collected from forest cover, 27.65% from rocky land, 29.41% from water body and 11.76% from barren land for further process (Figure 7). 

Figure 7. Ground Reference Triangle

b.  Statistical analysis

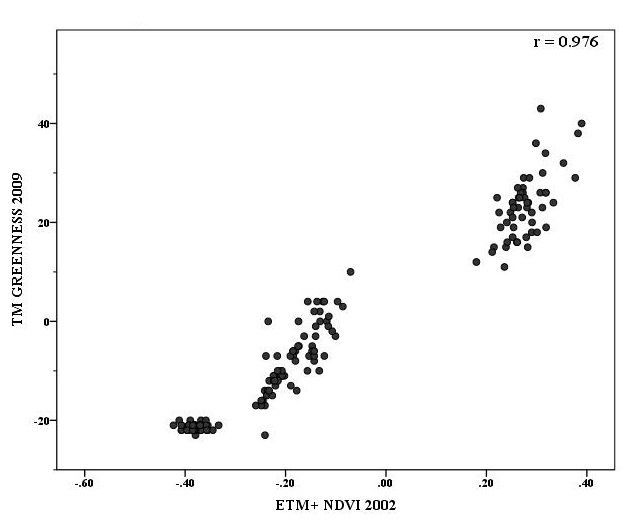
NDVI has been widely used for vegetation analysis, however, greenness (equation 5 and 6) (Crist et al., 1986; Huang et al., 2002) have more potential of vegetation analysis. Greenness values estimated for both images (t₁ and t₂) have positively correlated with NDVI. Therefore, greenness estimated for ETM+ (t₁) and TM (t₂) data was used as dependent variable for estimations corrected greenness values for t2 (Figure 8). 

Figure 8. Greenness Index

Greenness (ETM+) = ((Band1 * (-0.3344)) + (Band2 * (-0.3544)) + (Band3 * (-0.4556)) + (Band4 * (0.6966)) + (Band5 *(-0.0242)) + (Band7* (-0.2630))  (5)

Greenness (TM) = ((Band1*(-0.2728)) + (Band2*(-0.2174))+ (Band3 * (-0.5508)) + (Band4 * (0.7221)) + (Band5 *(0.0733)) + (Band7 * (-0.1648))    (6)

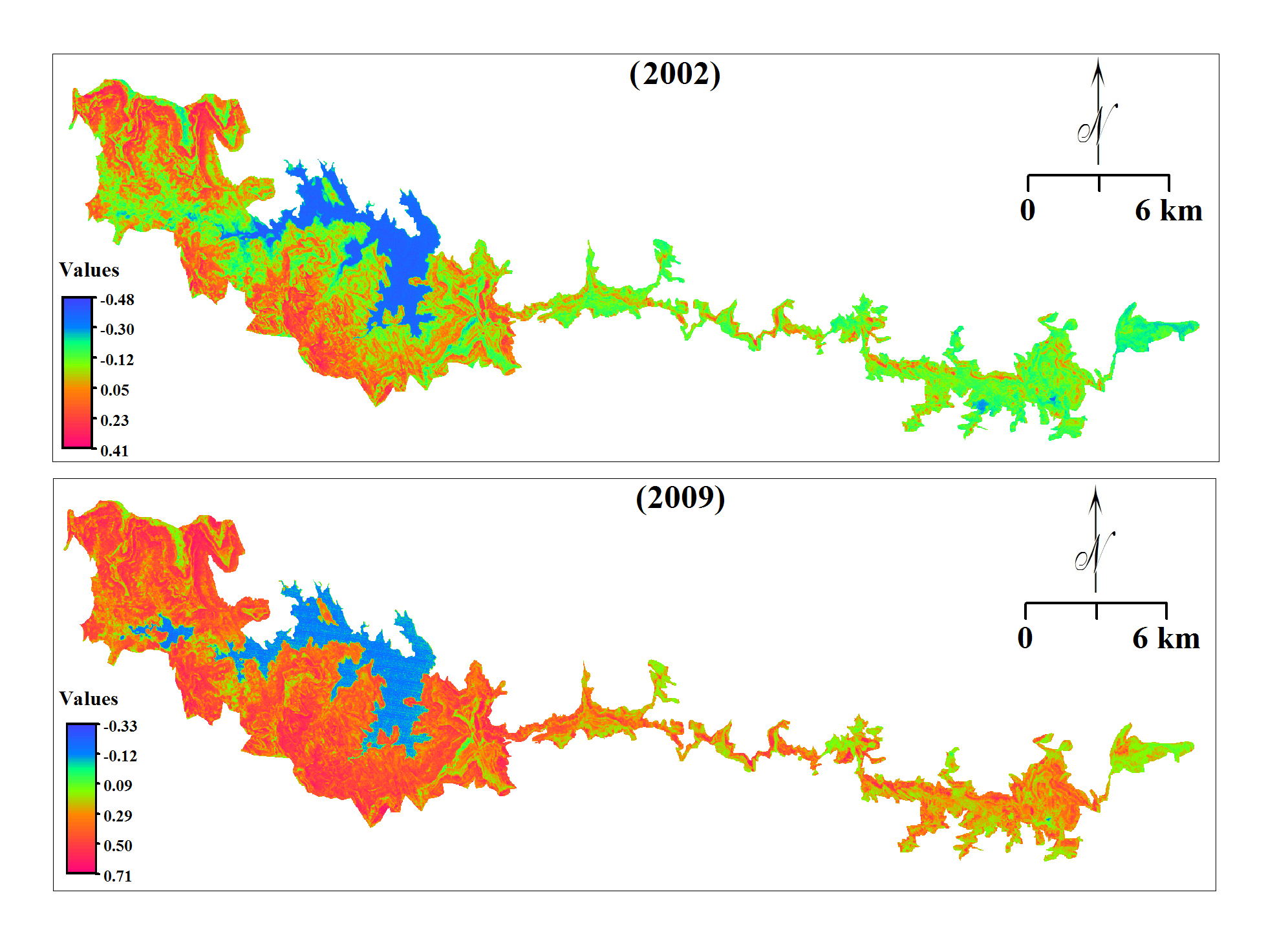
NDVI (2002) values show positive correlation with greenness estimated for t₂ (2009) (r = 0.976) and NDVI (2009) with greenness for t₂ (2009) (r = 0.975) (Table 6). Scatterplot (Figure 9) for NDVI (2002) and Greenness (2009) show clustered distribution of vegetation. Therefore, calculated greenness values used for estimations of dependent variable in regression analysis. Maximum greenness (-0.07) calculated for t₁ (2002) and 65.06 for t₂ (2009) whereas minimum (-110.16) for no-vegetation i.e. water, rocky land, shadow, etc. in t₁ (2002) and -36.57 in t₂ (2009). These are stable land surface in the study area. Theoretically, values estimated for the stable lands might be same which is not possible in certain conditions at the time of image capturing (Munyati, 2004; Yarbrough et al., 2005; Gill et al., 2012). Therefore, accuracy of FCD in the region shows less. Further, these estimated values have been normalized using values estimated for stable pixels in this approach. Differences between estimated greenness values for stable pixels of t₁ and t₂ have been calculated and correlation with estimated indices SWI (t₁), brightness (t₁), fifth (t₁) and DN values of band 7 (t₁), band 7 (t₂), band 5 (t₁) have been estimated to find independent variables for estimation of normalized dependent variable for t₂ e.g. greenness. 

Figure 9. Scatterplot: NDVI (2002) and Greenness (2009)

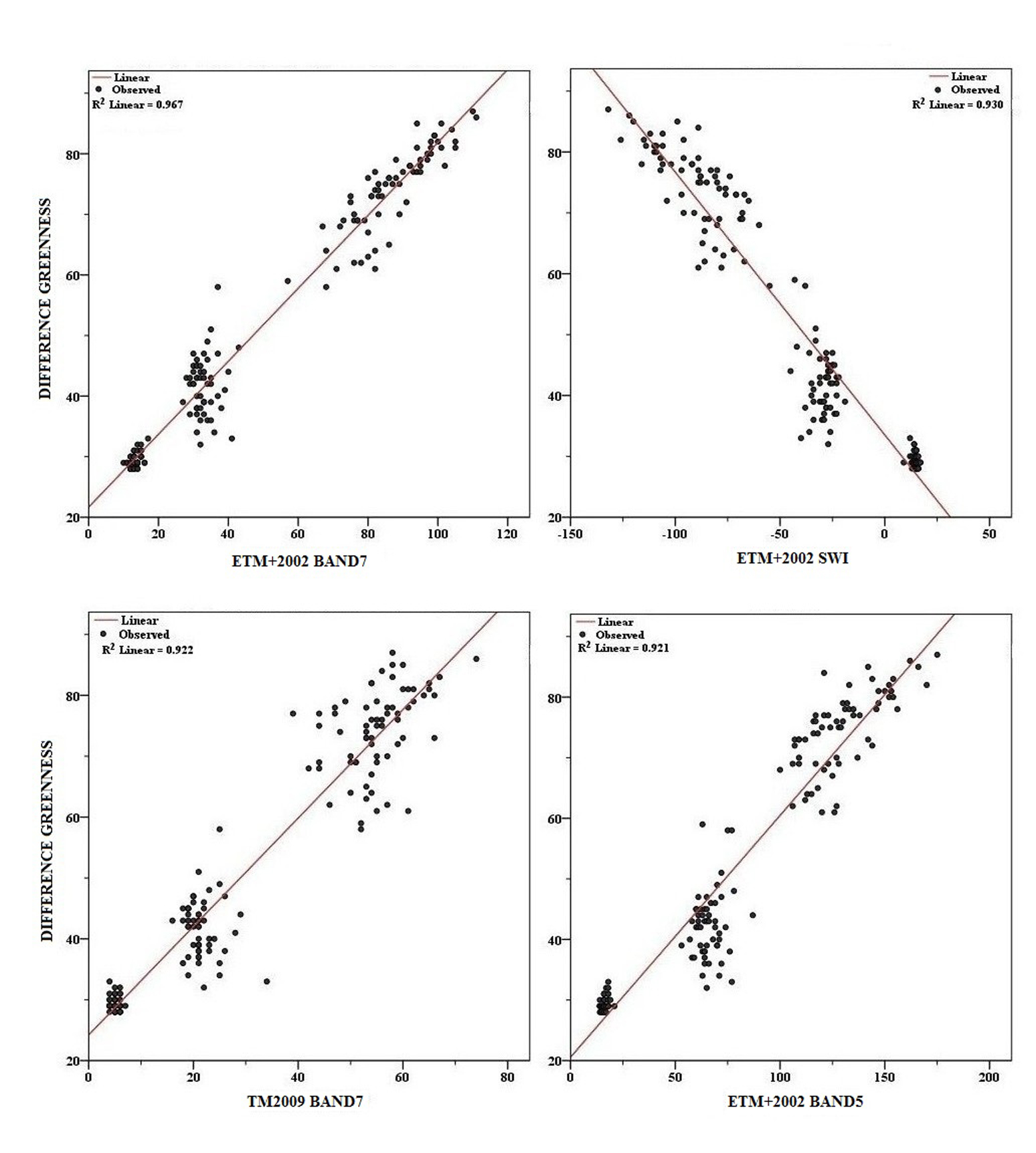
Significant correlation of calculated difference between greenness estimated for stable pixels of t₁ and t₂ was estimated with band 7 (t₁), SWI (t₁), band 5 (t₁) band 7 (t₂), brightness (t₁), difference in SWI, difference in fifth (Table 7). However, the strongest correlation was estimated for band 7 of t₁ and therefore this band was used as independent variable for estimations of pixel values of correction in t₂ using regression techniques. Samples (170) collected from stable land surface i.e. forest land, rocky land, water, barren land, etc. (Figure 7) was used for this analysis. 

Regression (equation 7) gives mathematical tools (Lawrence and Wrlght, 2001; Cohen et al., 2003) to estimate the fit between two different multi-spectral images acquired at different time for same area. Pixel values close to the regression line indicate the suitability of the model (Table 8).

  \(Y=a+b(x)\)                 (7)

Where, \(Y\)  is an estimated variable (dependent), \(a\)  and \(b\) are constant ( \(a\)  is intercept and \(b\)  is rate of change in slope) and \(x\)  is independent variable.

 Scholars have been reported the highest change detection accuracy by using regression approach. Jiany et al., (2008) reported three steps of radiometric normalization using pixel values for stable land surface: (1) delineation of stable land based on near-infrared (NIR) bands; (2) DN for stable areas using regression models, and (3) the regression coefficients used for normalizing DN of the target image. Here, linear regression model depicts (Figure 10) the fit (R²= 0.967) of differences in Greenness of t₁ and t₂ with band 7 of t₁ with high correlation (0.983) and clustered distribution. The values closer to zero on x-axis are for water bodies, next cluster for forests and at far from the zero for barren and rocky lands. Band 5 and band 7 of ETM+ and TM images show higher sensitivity to soils and vegetation.

Figure 10. Regression analysis

c.   Estimation of exaggeration and normalization of images

The maximum value (0.41) in reference image (t₁) (NDVI 2002) was observed for dense vegetation (Table 3) whereas minimum (-0.48) for barren land and water body with 0.05 mean and 0.16 standard deviation. Maximum NDVI value (0.71) in target image, (t₂) (2009) was observed for dense vegetation and minimum (-0.33) for no-vegetation with 0.31 mean and 0.16 standard deviation. Therefore, it is assumed that the values recorded in target image are exaggerated from ground reality (Figure 8). Regression model (equation 8) was formed to estimate the values of exaggeration in greenness (Ge) estimated for target image (t₂) for normalizing (t₂).

\(Ge=a+b(B7t_1)\)                                (8)

Where, \(a\)  is an intercept 21.664 and \(b\)  is rate of change in slope 0.602 and \(B7 t_1\)  is band 7 of reference image (t₁). Finally, raster image for greenness estimated for target image (t₂) was normalised \(Nt_2\)  (equation 9) for final FCD.

\(Nt_2=Greenness2009-Ge\)                    (9)

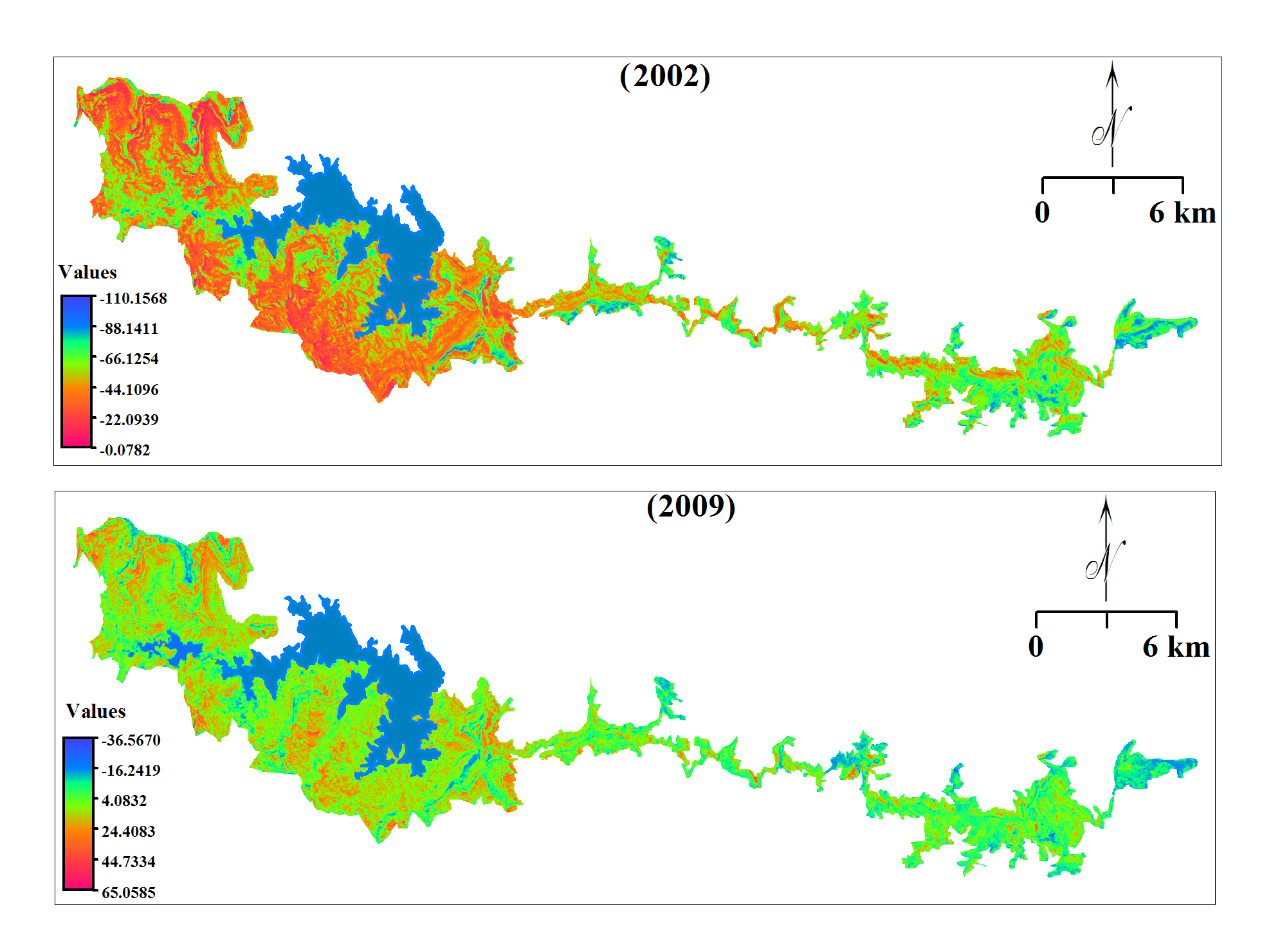
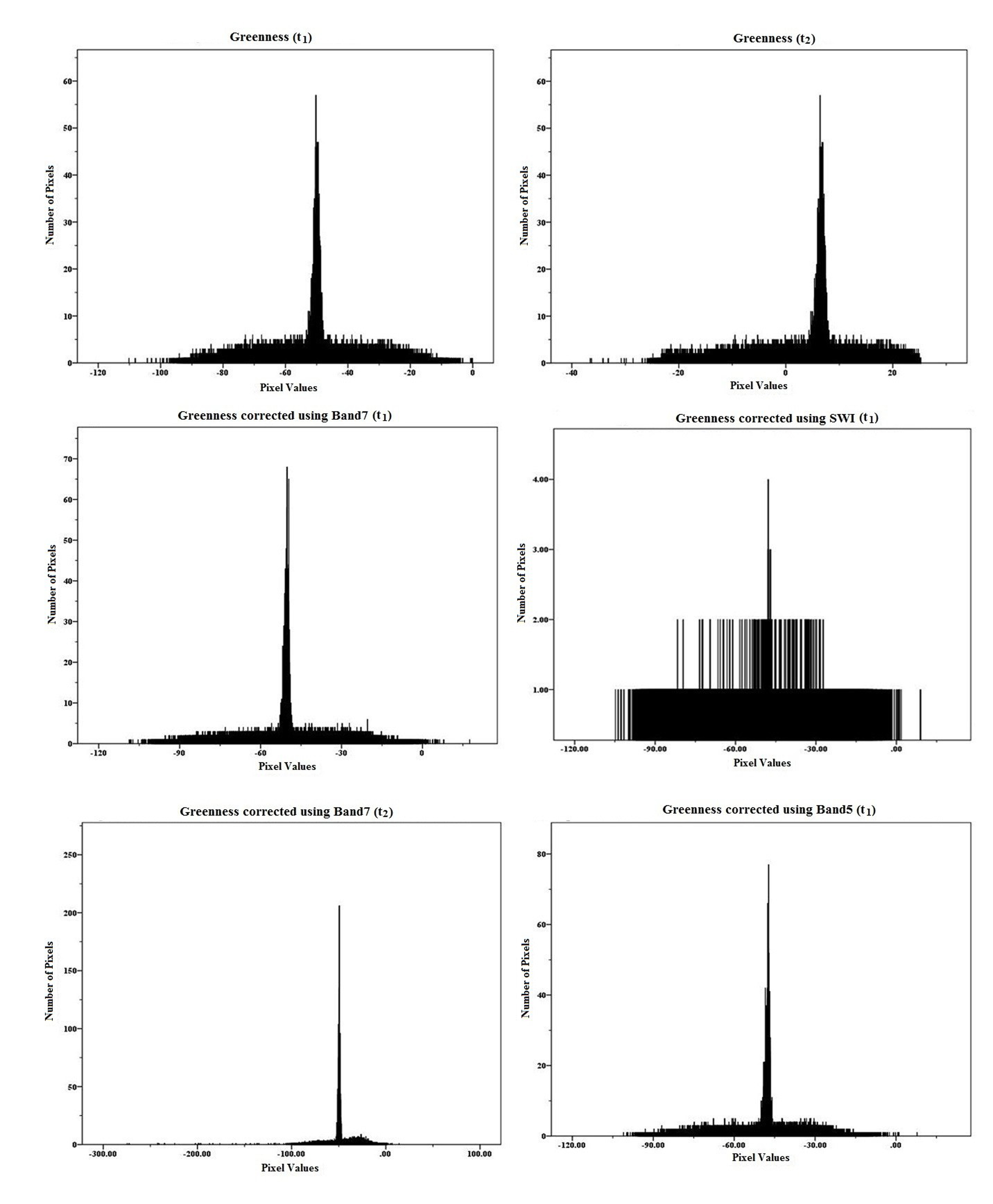
The histograms for estimated images viz. corrected greenness 2009 using band 7 (t₁), SWI (t₁), band 7 (t₂) and band 5 (t₁), etc. were prepared in SPSS and compared with histograms prepared for greenness for t₁ and t₂ (Figure 11). Histogram values distributed from -110.1568 to -0.0782 for greenness of ETM+ (2002) and from -36.5670 to 65.0585 of TM (2009). However, distributed values on histogram prepared for corrected greenness of t₂ (2009) vary from -108.6296 to 17.5085. Similar results observed for normalised raster images of band 7 (2002), SWI (2002), band 7 (2009) and band 5 (2002). 

Figure 11. Histogram distributions

4.3.3  Change detection

Finally, raster image of greenness estimated for t₁ (ETM+ 2002) and normalised raster image of greenness estimated (Figure 12) for t₂ (TM 2009) were processed for FCD in this study. The maximum value was -00.08 estimated for greenness of t₁ (2002) and 17.51 for normalized greenness (2009) whereas minimum value was -110.16 for t₁ (2002) and -108.63 for normalized image t₂ for ‘no-vegetation’ i.e. water, rocky land, shadow, etc. (Figure 13). Reference (t₁) and normalised (Nt₂) images were classified into five classes (Table 9) e.g. no-vegetation, low to medium, medium, medium to dense and dense to very dense, respectively.

Figure 12. Corrected Greenness index

Classified raster images (Figure 13) for 2002 and 2009 were combined using cross operation in Ilwis for forest CD. 25 classes were created in this combination and similar classes merged to get meaningful categories (Table 4). Overall changes were estimated as ‘negative changes’, ‘positive changes’ and ‘no-changes’. Further, class wise changes also estimated to know the transformations from one class to another (Table 5) as ‘positive change, negative change and no-change.

Figure 13. Distribution of forests depicted based on greenness index

5 . RESULTS

Changes in forest cover in the study area (13858.83 ha) was estimated using two approaches: Approach I) post-classification technique and Approach II) improved post-classification technique. NDVI based classified maps prepared for t₁ and t₂ were used for CD (Figure 14) in first approach and statistical analyses were performed for improvement in accuracy of post-classification CD in second approach (Figure 15). Primary field check data and pixel information of stable land units i.e. water bodies, deep forest and rocky lands were used in statistical analysis for improvement of the technique.

5.1  Approach I: Post-classification Technique

The change in forest area within period of images acquired has been detected and successfully demarcated (Figure 14). Approximately, 58.59% of reviewed area shows forests with increasing trends, 33.69% area shows no-changes and 7.72% area losing the forest. Forest cover increases for the class ‘medium’ vegetation about 22.41% and class ‘dense to very dense’ 16.84% (Table 10). Slightly negative change (-0.12%) observed for class ‘no-vegetation’ and the class ‘medium to dense’ (-2.81%) (Figure 14). Positive changes in forest cover was estimated for 8119.98 ha, no-change for 4669.29 ha and negative change for 1069.56 ha. However, these estimated values show generalized picture of changes within the classes therefore, dynamics of class wise changes also analyzed. 

Figure 14. Approach-I: distribution of changes in forest cover

Sparse vegetation has been changed to medium vegetation (22.68%) and dense vegetation to very dense vegetation (15.02%) (Table 11) with no-change on 10.89 % area. However, vegetation decreases with high rate from ‘low vegetation’ to ‘no-vegetation’ for 4.30% area. The accuracy of assessment has been estimated about 77.84%, discussed in the next section (Table 14).

5.2 Approach II: Improved Post-classification Technique

Statistical techniques i.e. correlation analysis and regression model have been used to improve the performance of FCD (Figure 6). Area under forest has been detected and estimated using TCCT greenness index. However, estimated greenness has been corrected to reduce exaggeration in reflectance recorded in DN using regression model (Figure 15). About 13858.83 ha (23.59% TGA) shows positive changes, 70.8% no-change and only 6.33% area shows negative changes. Accuracy assessment shows preciseness 95.21% (Table 15) of the results compared to post-classification based FCD. ‘No-changes’ in vegetation observed for the class, ‘low to medium’ vegetation (Table 12) and positive changes for ‘medium to dense’ and ‘dense to very dense’ vegetation. This improved technique of FCD helps to reduce the exaggeration in estimations. Class wise changes also estimated to understand the dimensions of changes in forest cover (Table 13). 

Figure 15. Approach-II: distribution of changes in forest cover

6 . ACCURACY ASSESSMENT

Accuracy of detected changes in forest cover was estimated as user’s accuracy, producer’s accuracy and overall accuracy. Rahman and Saha (2008) have suggested that the sample size should take minimum 30 for each class to estimate accuracy at 90%. Therefore, 170 samples well distributed within the classes were collected using GPS points and Google Earth Pro high resolution images.

Overall accuracy of the FCD using approach I: post-classification technique was estimated about 77.84% (Table 14). User’s accuracy was estimated about 58% for positively changed forest cover, 70% for no-changed or stable and 80% for negatively changed forest and 96% for water bodies. Producer’s accuracy was estimated about 70% for positive changes, 78% for no-changes, 76% for negative changes and 83% for water bodies. Maximum accuracy was estimated for water bodies and negative changes in vegetation whereas positively changed vegetated area and stable land units show very less accuracy. Accuracy assessment suggests need of improvement in FCD techniques. Therefore, algorithm for improved FCD has been formulated in this study. Approach II has improved accuracy of FCD to 95.21% (Table 15) with user’s accuracy about 97% for positive changes, 95% for no-change, 93% for negative changes and 96% for water bodies. Producer’s accuracy was estimated about 91% for positive changes, 98% for no-change, 95% for negative changes and 96% water bodies. Thus, improved post-classification technique improves the accuracy of FCD.

7 . CONCLUSION

About 58.59% of reviewed area estimated using first approach of CD shows (Figure 15) positive changes, 33.69% no-change and 7.72% negative changes in forest cover in the area. However, improved post-classification analysis estimates (Table 16) about 23.59% area with positive changes, 70.08% no-change and 6.33% negative changes. Thus, normalised raster greenness image using statistical analysis removes illusional exaggeration of reflectance recorded in satellite data and useful to estimate more precisely FCD.

Authors are aware about limitations of finer temporal resolution (7 years) and medium spatial resolution (30 x 30m) of Landsat ETM+ and Landsat TM images. The methodology and techniques formulated in this study can be useful for researchers, scholars, environmental planners and managements for change detection of forest for sustainable land management and development.

Tables

Figures

Conflict of Interest

Acknowledgements

Abbreviations

References